No results found

Project

Structure in Prime Gaps - Formalized

STRUCTURE IN PRIME GAPS - FORMALIZED

PROJECT PROPOSAL

prepared for: https://leanprover.zulipchat.com/

prepared by: KAJANI KAUNDA

Let us lean together! 

import Mathlib.Data.Nat.Prime.Basic
import Mathlib.Data.List.Basic
import Mathlib.Tactic.Linarith
import Mathlib.Data.Int.Defs
import Mathlib.Tactic.Basic

open List Nat

-- Define the set of primes and their additive inverses
def primes_and_inverses : List ℤ :=
  (List.range 100).filter Nat.Prime |>.map (λ p => [↑p, -↑p]) |> List.join

-- Construct the Cayley table T for a finite portion
def cayley_table (n : ℕ) : List (List ℤ) :=
  let primes := (List.range n).filter Nat.Prime |>.map (λ p => ↑p)
  let inverses := primes.map (λ p => -p)
  let first_row := primes
  let first_column := inverses
  let table := first_column.map (λ inv => first_row.map (λ p => p + inv))
  first_row :: table

-- Example of using the cayley_table with a finite portion
def T : List (List ℤ) := cayley_table 30

#eval T -- To visualize a portion of the table

Structure in Prime Gaps -- Formalized

By Kajani Kaunda, Jane Doe, John Doe, and others.

Abstract

In this open community project, we formalize using the LEAN programming language, the definitions and results presented in the paper Structure in Prime Gaps.

Introduction

Remark: In this paper, we will dispense with a lot of contextual explanations and restrict ourselves only to those which are pertinent to the formalization process.

Formalization of Mathematics.

The formalization of mathematics refers to the process of encoding mathematical definitions, theorems, and proofs in a formal language that can be processed and checked for correctness by a computer. This approach ensures that every logical step is explicitly verified, leaving no room for ambiguity or human error. This meticulous approach ensures that every logical step is explicitly defined and verified, minimizing the risk of human error in mathematical proofs. The goal is to achieve a level of rigor and precision that surpasses traditional mathematical methods, enabling the verification of complex proofs and the discovery of new mathematical insights. Formalization not only helps in validating existing results but also provides a robust framework for discovering new ones.

Proof Assistants.

Proof assistants are software tools designed to aid in the creation and verification of formal proofs. These tools provide a platform for writing proofs in a formal language and automatically verifying their correctness. They offer a rigorous environment where users can construct proofs interactively or automatically, depending on the complexity of the problem. These tools are essential in modern mathematics and computer science, allowing for the development of highly reliable software and the verification of intricate mathematical theorems. Popular proof assistants include Coq, Isabelle, and Lean. There are many others. They are used not only in pure mathematics but also in fields like computer science, where formal verification of software and hardware is crucial. They have been instrumental in formalizing significant results across various domains.

LEAN.

LEAN is a modern open-source proof assistant developed at Microsoft Research. It stands out for its user-friendly interface and powerful capabilities in both theorem proving and automated reasoning. It is designed to support the formalization of mathematics and the verification of software. LEAN supports a rich type theory known as dependent type theory, which allows for expressive and concise representations of mathematical objects and proofs. Its growing ecosystem includes a standard library of formalized mathematics and tools like the LEAN community web editor. LEAN has been adopted by many mathematicians and computer scientists for both educational purposes and advanced research projects. LEAN combines powerful automation with interactive proof development, making it accessible to both beginners and experts. LEAN 4, the latest version, offers significant improvements in performance and usability, encouraging more widespread adoption within the mathematical community.

Structure in Prime Gaps.

In this project, we aim to formalize the results presented in the article Structure in Prime Gaps using LEAN 4, the latest version of the LEAN proof assistant. By leveraging the capabilities of LEAN 4, we seek to ensure the correctness and robustness of these findings relating to the existence of infinitely many structured gaps between prime numbers. This formalization will provide a rigorous foundation for the results and contribute to the broader effort of formalizing mathematics.

The paper Structure in Prime Gaps presents two main results the first of which is the claim that there exist structured gaps between primes and the second result is basically a corollary or special case of the first. These are stated as follows:

Theorem 1: For every prime pα, there exists infinitely many pairs of primes, (pn, pn+m), such that (pn+m − pn) = pα − 3, where n, α ≥ 3, m ≥ 1, and pn is the nth prime.

Theorem 2: There exist infinitely many pairs of primes with a gap of 2.

A brief visual overview of the results presented in the article Structure in Prime Gaps

The following partial Cayley table T represents gaps between primes in which the results we are formalizing are self-evident.

Consider Table 1, it is not immediately apparent if any useful pattern can be discerned from it. However, with the highlights in Table 2, a compelling pattern emerges, one that leads directly to Theorem 1 from which Theorem 2 is implied as seen in Table 3.

  • Each pattern is defined and identified by the 4-tuple β = (A, B, L, E) formed from the elements in the vertices of a sub-array Ti of T. In Table 2, the first 4-tuple β = (A, B, L, E) for prime 23 is β = (20, 28, 12, 20).

  • Every sub-array TTi, defines two pairs of primes. In Table 2, the First pair is (3, pα) or (3, 23) and the Second pair is (((B + 3) + 0 -- E), (B + 3)) or (11, 31). We can denote the integers 11 and 31 in the Second pair using the variables Qi and Ri respectively.

  • The First pair remains constant for all patterns related to any prime pα ≥ 5. Subsequent Second pairs are unique for each sub-array TTi of T.

  • L is always congruent to 0 mod 6.

Legend for Tables:

  • Table 1: Represents the Cayley Table T of the Commutative Partial Groupoid structure (J, +) without immediately discernible patterns highlighted.

  • Table 2: Highlights patterns where the 4-tuple β = (A, B, L, E) defines each pattern, with specific examples provided. The "Pattern" here is more elaborately defined in the sense that it consists of integers other than just Qi and Ri.

  • Table 3: Demonstrates the implication of results derived from the patterns observed in Table 2.

  • Remark: We note that the Cayley Table T is a partial representation of an otherwise infinite structure. Therefore no generalization of these results to some "complete/larger" set is required.

Table 1

Table Legend

Table 2

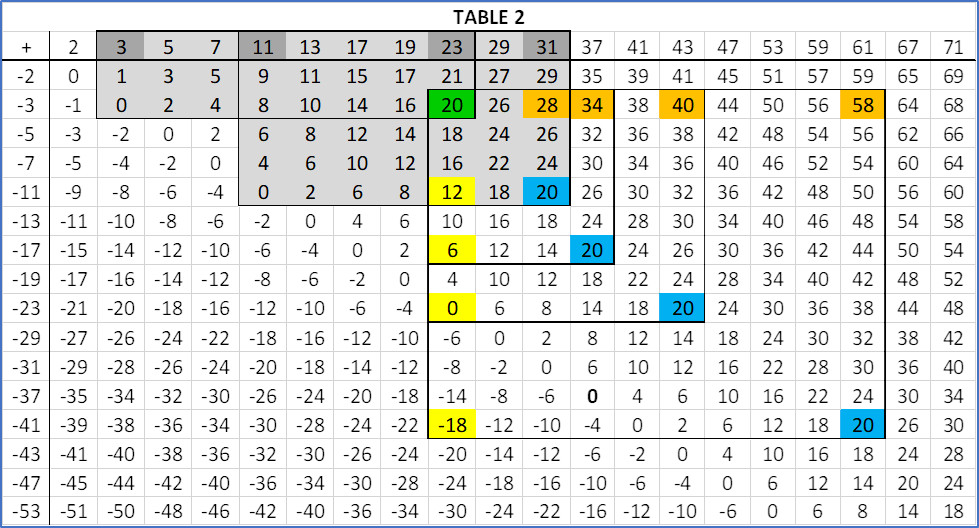
Table 3

Definitions and results to be Formalized

The final LEAN 4 code will most likely be different from the following code snippets but at the very least it is good to know and verify that formalization is possible with the current technology stack; LEAN 4 and the Mathlib library.

We begin as follows:

Item name

Definition 1.

Formal statement

Definition 1: Define a model of prime gaps as a Cayley Table T constructed from a Cummutative Partial Groupoid (J, +) based on a subset J of Z containing the infinite set of prime numbers and their additive inverses, such that the elements of the first row of T are the primes and the elements of the first column of T are their additive inverses.

Notes

The set J is defined as follows J = (...,−pn+2, −pn+1, −pn, pn, pn+1, pn+2, ...). Notice that since primes are infinite then by definition the structure T is also infinite. The structures used by LEAN 4 in defining T must reflect this property.

LEAN 4 code

import Mathlib.Data.Nat.Prime.Basic
import Mathlib.Data.List.Basic
import Mathlib.Tactic.Linarith
import Mathlib.Data.Int.Defs
import Mathlib.Tactic.Basic

open List Nat

-- Define the set of primes and their additive inverses
def primes_and_inverses : List ℤ :=
  (List.range 100).filter Nat.Prime |>.map (λ p => [↑p, -↑p]) |> List.join

-- Construct the Cayley table T for a finite portion
def cayley_table (n : ℕ) : List (List ℤ) :=
  let primes := (List.range n).filter Nat.Prime |>.map (λ p => ↑p)
  let inverses := primes.map (λ p => -p)
  let first_row := primes
  let first_column := inverses
  let table := first_column.map (λ inv => first_row.map (λ p => p + inv))
  first_row :: table

-- Example of using the cayley_table with a finite portion
def T : List (List ℤ) := cayley_table 30

#eval T -- To visualize a portion of the table

LEAN 4 code annotation

Item name

Definition 2.

Formal statement

Definition 2: Define a v x w sub-array TTi of T such that v, w ≥ 2.

Notes

Definition 2 defines a sub-array which is later used to algebraically construct a pattern.

Example: TT1 = ((2, 4, 8, 10), (0, 2, 6, 8), (-2, 0, 4, 6), (-6, -4, 0, 2)).

LEAN 4 code

-- Define a sub-array TTi of T, where v x w are its dimensions
def sub_array (T : List (List ℤ)) (r c v w : ℕ) : List (List ℤ) :=
  (T.drop r).take v |>.map (λ row => (row.drop c).take w)

-- Example: Extract a 3x3 sub-array from T
def TT1 : List (List ℤ) := sub_array T 1 1 3 3

#eval TT1 -- Visualize the sub-array

LEAN 4 code annotation

Item name

Definition 3.

Formal statement

Definition 3: Define a 4-tuple β = (A, B, L, E) such that the values of its elements are the vertices of TTi.

Notes

This is one of the structures used in the analysis of T.

Example: for TT1, we have TT1.β = (2, 10, -6, 2).

LEAN 4 code

-- Define the structure for the 4-tuple β
structure Beta where
  A : ℤ
  B : ℤ
  L : ℤ
  E : ℤ

-- Create a 4-tuple β from the vertices of a sub-array TTi
def create_beta (TTi : List (List ℤ)) : Beta :=
  ⟨TTi.head!.head!, TTi.head!.getLast!, TTi.getLast!.head!, TTi.getLast!.getLast!⟩

--- -- Provide a Repr instance for Beta to define how it should be displayed
--- instance : Repr Beta :=
---  ⟨fun β => s!"⟨{β.A}, {β.B}, {β.L}, {β.E}⟩"⟩

-- Example usage: Create β for TT1
def β1 : Beta := create_beta TT1

--- #eval β1 -- Visualize β1

#eval β1.A -- Visualize β1
#eval β1.B -- Visualize β1
#eval β1.L -- Visualize β1
#eval β1.E -- Visualize β1

LEAN 4 code annotation

Item name

Lemma 4.1. This is the first Lemma.

Formal statement

Lemma 4.1 : Prove that: Given a 4-tuple β then A + E = B + L.

Notes

This is one of the results used in the subsequent proofs.

The proof is derived from the construction of T.

LEAN 4 code

lemma lemma_4_1 (m n c k : ℤ) :
  let TTi_A := m + n
  let TTi_B := m + (n + k)
  let TTi_L := (m + c) + n
  let TTi_E := (m + c) + (n + k)
  TTi_B + TTi_L = TTi_A + TTi_E :=
by
  -- Expand and simplify the expressions
  linarith

LEAN 4 code annotation

Item name

Lemma 4.2. This is the second Lemma.

Formal statement

Lema 4.2 : Prove that: All prime numbers greater than 3 can be expressed in the form 6n + 1 or 6n − 1.

(A known result).

Notes

This result is used in the subsequent proofs.

LEAN 4 code

LEAN 4 code annotation

Item name

Lemma 4.3. this is the third Lemma.

Formal statement

Lemma 4.3: Let tm,n be a term in T where the indexes m and n are zero based and refer to the rows and columns in T respectively.

Prove that:

For every prime pα ≥ 5, there exists a sub-array TTi ∈ T such that the following properties are simultaneously true;

Property 1 : TTi.A + 3 ∈ {6n ± 1|n ∈ N1}

Property 2 : (TTi.B + 3) − TTi.E ∈ {6n ± 1|n ∈ N1}

Property 3 : TTi.L ≡ 0 (mod 6)

Property 4 : TTi.A = TTi.E

Property 5 : TTi.B + 3 ∈ {6n ± 1|n ∈ N1}

If and only if

for TTi.A + 3 ∈ {6n − 1|n ∈ N1};

TTi.A = 6x + 6y − 4

TTi.B = 6x + 12y − 8

TTi.L = 6x

TTi.E = 6x + 6y − 4

for TTi.A + 3 ∈ {6n + 1|n ∈ N1};

TTi.A = 6x + 6y − 2

TTi.B = 6x + 12y − 4

TTi.L = 6x

TTi.E = 6x + 6y − 2

where n ∈ N1, x < n, y > 0, n = x + y, (TTi.A + 3) = pα and TTi.A = t2,k.

Notes

This result demonstrates the existence of a pattern. It algebraically shows that for every prime pα ≥ 5, there is a pattern TTi that defines a pair of integers Qi and Ri such that Ri − Qi = pα − 3.

The key in the proof of this result is the following analysis:

  • We are given pα as a constant quantity.

  • Now pα can be expressed in the form 6n ± 1.

  • This implies that n in the expression 6n ± 1 is constant.

  • We then let n = x + y.

  • We then use combinatory analysis to heuristically determine which expressions to assign to A, B, L and E from the sets M = (6x, 6y, -4, 6x, 6y, -4) and N = (6x, 6y, -2, 6x, 6y, -2) such that the five (5) properties of Lemma 4.3 are satisfied.

But how are the sets M and N derived?

Notice that by Lemma 4.3, TTi.A = TTi.E and (TTi.A + 3) = pα. Since pα is prime then it can be expressed in the forms 6n ± 1 or 6(x + y) ± 1. And by Lemma 4.1, A + E = B + L, which implies that TTi.B + TTi.L = TTi.A + TTi.E = ((6x + 6y + -4) + (6x + 6y + -4)) or ((6x + 6y + -2) + (6x + 6y + -2)) depending on which form pα can be expressed.

LEAN 4 code

LEAN 4 code annotation

Item name

Lemma 4.4. This is the fourth Lemma.

Formal statement

Lemma 4.4: Let any sub-array TTi that satisfies Lemma 4.3 be referred to as a Prime Array.

Prove that: For every prime pα ≥ 5, there are infinitely many Prime Arrays such that TTi.A = pα − 3.

Notes

This will show that for any prime pα ≥ 5 the pattern defined by the Prime Array TTi occurs infinitely often and that consequently, the integer pairs (Qi, Ri) also occur infinitely often.

The key in the proof is to show that for any prime pα ≥ 5,

  • pα is constant.

  • Which implies n is constant.

  • But n = x + y

  • Now changing the value of y changes the value of x in order to maintain the equality n = x + y.

  • Changing the value of x changes the value of L since L = 6x.

  • Changing the value of L changes the value of B since B + L = A + E and A + E is a constant expression.

  • This implies that the value of y can be changed infinitely often and each change represents a different sub-array or Prime Array TTi.

LEAN 4 code

LEAN 4 code annotation

Item name

Lemma 4.5. This is the fifth Lemma.

Formal statement

Lemma 4.5: Prove that: For every prime pα ≥ 5, there exists infinitely many Prime Arrays, TTi, such that TTi.A = pα − 3 and (Ti.B + 3) and ((Ti. B + 3) −Ti.E) are prime.

Notes

This will show that for any prime pα ≥ 5, the Prime Arrays TTi occur infinitely often and Qi and Ri are prime. Notice that here, (TTi.B + 3) = Ri and Qi = ((TTi.B + 3) − TTi.E).

The proof here relies on the construction of T where all the elements on the first row of T are prime

We can then algebraically show that (TTi.B + 3) and ((TTi.B + 3) − TTi.E) are prime.

LEAN 4 code

LEAN 4 code annotation

Item name

Theorem 1. The first Theorem, the first of the two main results.

Formal statement

Theorem 1: Prove that: For every prime pα, there exists infinitely many pairs of primes, (pn, pn+m), such that (pn+m − pn) = pα − 3, where n, α ≥ 3, m ≥ 1, and pn is the nth prime.

Notes

The claim is that this result is implied from the previous results as demonstrated in the following steps:

Step 1: By Lemma 4.5, and the construction of T, TTi.A and TTi.E are prime gaps.

Step 2: By Lemma 4.3, TTi.A = TTi.E.

This is equivalent to: (TTi.A + 3) − 3 = ((TTi.B + 3) − ((TTi.B + 3) − TTi.E)).

Step 3: By Lemma 4.5, the following are prime; (TTi.A + 3), ((TTi.B + 3) − TTi.E), (TTi.B + 3).

Step 4: By Lemma 4.5, for every prime (TTi.A + 3) ≥ 5, there are infinitely many of the following pairs of primes defined as: (((TTi.B + 3) − TTi.E), (TTi.B + 3)).

We can then see that the following statement is implied:

For every prime (TTi.A + 3) ≥ 5, there exists infinitely many pairs of primes, (((TTi.B + 3) − TTi.E), (TTi.B + 3)), such that ((TTi.B + 3) − ((TTi.B + 3) − TTi.E)) = (TTi.A + 3) − 3.

This statement is equivalent to the formal statement of Theorem 1 which can be is re-stated using the following equivalent assignments:

pα − 3 = TTi.A.

pn+m − 3 = TTi.B.

pα − pn = TTi.L.

pn+m − pn = TTi.E.

LEAN 4 code

LEAN 4 code annotation

Item name

Theorem 2. This is the second Theorem, the second of the two main results.

Formal statement

Theorem 2: Prove that there exist infinitely many pairs of primes with a gap of 2.

Notes

This result is just a special case of Theorem 1 when pα is set to 5. I am sure this would be resolved by LEAN 4 using the "refl" similar tactic.

LEAN 4 code

LEAN 4 code annotation

Outcome and Conclusion

By formalizing the results presented in the paper Structure in Prime Gaps, we hope to contribute to the body of knowledge in mathematics as well as help establish the use of proof assistants like LEAN in academia, research and industry in general.

Source References

Useful Links